The ESG-efficient frontier (Part I)
This week we look at a paper that proposes a framework known as the ESG-efficient frontier
This week, we will look at a paper by AQR’s Lasse H Pedersen, Shaun Fitzgibbons and Lukasz Pomorski. This paper was published in 2019 (about four years old now) but it is an influential one in that it contains some really useful ideas on how to incorporate ESG in a portfolio optimization problem.
Why do we care about this? Well, if you are managing a portfolio and need to integrate ESG preferences into your investment process, it helps to get a sense of the thinking behind the ESG-efficient frontier to help you with deciding on an optimal portfolio.
Even if you doesn’t care about ESG, it is probably helpful to understand the thinking of investors who express an ESG preference in their portfolios.
This paper is rather long so it will be split into two parts. In this post, we will cover the theory behind the ESG-efficient frontier. In the next post, we will look into some empirical results.
Let’s begin!
What is an ESG-efficient frontier
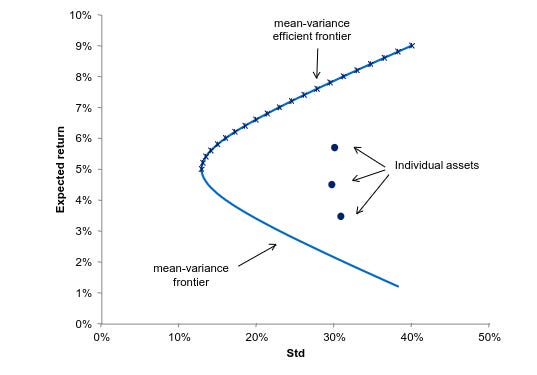
Before we start, it is probably worth asking what is even a standard efficient frontier. To put it simply, it is a curve that contains a combination of assets that offers the highest level of expected returns for each level of risk.
For example:
As an investor, you can choose any points along the curve (or line or frontier — they all refer to the same thing) in the upper part to maximize your expected returns for each level of risk (or standard volatility). Notice that the upper part is known as efficient frontier because for a given level of risk, you can get a higher expected return.
There is also a concept known as the tangency portfolio, the point where the Capital Market Line (CML) is tangential to the frontier. The CML represents the risk-return trade-off for a portfolio with a risk-free asset and a risky portfolio. we have the highest ratio of expected returns to risk. You may also recognize this as the point where we would have the maximum Sharpe Ratio, which is simply the risk-adjusted return.
For instance, choosing the tangency portfolio above may mean your optimal portfolio would be a combination of a risk-free asset that provides 2% expected return and a risky portfolio. You would expect the portfolio to produce a Sharpe Ratio that is equal to the slope labeled above.
From here, we can extend into the concept of an ESG-efficient frontier, which uses ESG score as the x-axis and Sharpe Ratio (SR) as the y-axis.
Let’s explain the diagram above a little bit more. Looking at the point labeled as Tangency portfolio using ESG information, this simply means the tangency portfolio in the earlier mean-variance efficient frontier, which has the highest SR, is now transported to the peak of ESG-efficient frontier.
What about the other points along the ESG-SR and ESG-efficient frontier then? Well, these are calculated by the same process, so we just repeat the process but now restrict the portfolio to have a certain ESG score.
This is an example to illustrate the ESG-efficient frontier, so the numbers are just a guideline. What is important to learn here is that the ESG-efficient frontier is hump shaped, with the highest-SR portfolio at the peak. And from that point out, having a preference to increase of decrease ESG score would result in a lower SR because we are adding a restriction to the portfolio to have any ESG score other than the peak-SR portfolio. Here is the ESG-efficient frontier again to capture the points in this paragraph:
Choosing portfolios using the ESG-SR frontier
To recap from the previous section, we started from the standard mean-variance efficient frontier and arrived at an ESG-SR frontier above.
Notice that the point beyond the peak SR, the line is now called the ESG-efficient frontier, as investors with an ESG preference may choose his or her optimal portfolio based on the trade-off between SR and ESG score. For instance, an ESG-motivated investor may choose point M below:
Even though Point M is not the highest SR portfolio, because the investor is ESG-motivated, he or she gains utility by having a higher ESG-score portfolio. For this type of investor, the maximum utility is thus gained at point M.
However, for another investor, who uses ESG information to build the ESG-SR frontier but derives all utility from returns, the portfolio chosen would be point A:
An investor who does not take into account of ESG score in building the efficient frontier, may get a different curve from the above, but would also select the highest SR portfolio.
Using an ESG-SR efficient frontier framework, we can therefore gain some insights into how investors may select the optimal portflio based on their ESG preference, which defines their utility function.
This may seem like a convulated way of saying some investors are willing to sacrifice returns for higher ESG scores, but this framework provides a way to quantify this preference and has some interesting empirical results, which we will cover in the next post.
To recap, the ESG-efficient frontier uses a standard mean-variance frontier to derive a set of optimal portfolios (with the highest SR based on the same risk-free asset) for each level of ESG score. This frontier then allows investors to choose the trade-off between SR and ESG score.